Relations de commutation

Comme pour les translations , les relations de commutation des composantes $L_x,~L_y$ et $L_z$ du moment cinétique total vont se déduire des propriétés du groupe des rotations. En effet, considérons à nouveau la rotation précédente :

$$R=R_x(\delta)\,R_y(\varepsilon)\,R_x(-\delta)\,R_y(-\varepsilon)$$

La rotation induite correspondante das l'espace de configuration s'écrira :

$$\mathcal{R}=e^{-i\,\delta\,L_x}\,.\,e^{-i\,\varepsilon\,L_y}\,.\, e^{i\,\delta\,L_x}\,.\,e^{i\,\varepsilon\,L_y}$$

Au premier ordre $\mathcal{R}$ est égal à 1, mais ici encore, en développant les exponentielles jusqu'au second ordre, on obtient :

$$\mathcal{R}=\mathbf{1}-\frac{\delta\,\varepsilon}{\hbar^2}\, (L_x\,L_y-L_y\,L_x)$$

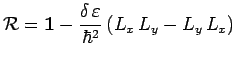Or, il a déjà été démontré :

$$R=R_z(\delta\,\varepsilon)~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{d'o\gra... ...thcal{R}_z(\delta\,\varepsilon)= e^{-\frac{i}{\hbar}\,\delta\,\varepsilon\,L_z}$$

En identifiant les deux expressions ainsi obtenues pour $\mathcal{R}$ , on obtient :

$$L_x\,L_y-L_y\,L_x=i\,\hbar\,L_z$$

On démontre ainsi les relations générales de commutation des composantes du moment cinétique d'un système :

$$\fbox{$ \begin{array}{ccc} & & \\ ~~~~~\left[ L_x , L_y \rig... ... \right] & = & i \, \hbar \, L_y~~~~~ \\ & & \\ \end{array}$}$$

Question 3-15 : Effectuez le calcul d'identification des deux expressions de $\mathcal{R}$ indiquées ci-dessus.

On remarquera que ces relations de commutation ne sont pas des propriétés spécifiquement quantiques, mais des conséquences des propriétés des rotations. C'est parce que les rotations sont des opérations géométriques qui ne commutent pas, que les composantes du moment angulaire sont des observables qui ne commutent pas non plus. On notera toutefois que l'apparition du coefficient $\hbar$ est une caractéristique spécifiquemet quantique.

Question 3-16 : Montrez que les états propres d'impulsion $\mid \vec{p}>$ sont invariants par translation et que les états propres du moment cinétique $\mid \ell,m>$ sont invariants par rotation.

Question 3-17 : Montrez que dans une rotation d'angle $\varphi$ autour d'un axe $O\vec{z}$ l'observable $P_x$ est transformée en l'observable $P_u$ avec :

$$P_u=\cos\varphi\,P_x+\sin\varphi\,P_y$$

Question 3-18 : Montrez que dans une rotation d'angle $\varphi$ et d'axe $O\vec{z}$ , l'état d'impulsion $\vec{p}$ est transformé en l'état d'impulsion $\vec{p}^\prime$ soit :

$$\mid \vec{p}^{\,\prime}>\,=\,\mathcal{R}_z(\varphi)\,\mid \vec{p}>~~~~~~~~~~~~~~~~~~~~~~~~\vec{p}^{\,\prime}\,=\, R_z(\varphi)\vec{p}$$