Les états propres de ![]() :
:
![]() admettent pour fonction d'onde :
admettent pour fonction d'onde :
mais les ![]() de Dirac ne sont pas de véritables fonctions.
Néanmoins la décomposition spectrale d'un ket quelconque :
de Dirac ne sont pas de véritables fonctions.
Néanmoins la décomposition spectrale d'un ket quelconque :
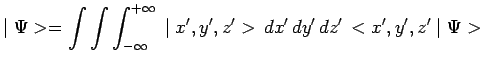 |
peut être transcrite ``chez Schrödinger'' comme suit :
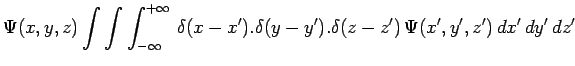 |
ce qui constitue d'ailleurs une identité en raison de la
signification fonctionnelle des ![]() de Dirac sous le signe d'intégration.
de Dirac sous le signe d'intégration.
Quelles sont les fonctions d'onde représentatives ``chez Schrödinger'' des
états propres d'impulsion ? L'équation aux valeurs propres écrite ``chez
Dirac'' selon :
est transcrite ``chez Schrödinger'' selon :
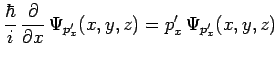 |
l'indice inférieur
![]() indiquant que la fonction d'onde
cherchée est relative à la valeur propre
indiquant que la fonction d'onde
cherchée est relative à la valeur propre
![]() de l'observable
de l'observable ![]() .
Cette dernière équation s'intègre parfaitement :
.
Cette dernière équation s'intègre parfaitement :
![]() désignant une fonction quelconque des variables
désignant une fonction quelconque des variables ![]() et
et ![]() . Il en résulte que la fonction d'onde représentative d'un état
propre simultané des trois observables
. Il en résulte que la fonction d'onde représentative d'un état
propre simultané des trois observables
![]() sera de la forme :
sera de la forme :
correspondance que l'on peut écrire :
la constante
![]() ayant pour objet de normaliser ces
états d'impulsion selon :
ayant pour objet de normaliser ces
états d'impulsion selon :
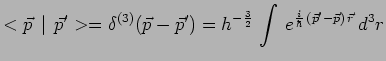 |