Nous savons déjà que
![]() constituent un E.C.O.C.
dont les états propres communs
constituent un E.C.O.C.
dont les états propres communs
![]() constituent une nouvelle base de représentation :
constituent une nouvelle base de représentation :
analogue à celle de Schrödinger :
Le même état ket
![]() peut être représenté
par la fonction d'onde
peut être représenté
par la fonction d'onde
![]() sur la base
sur la base
![]() ou par la fonction d'onde
ou par la fonction d'onde
![]() sur la
base
sur la
base
![]() . La correspondance entre ces deux
représentations s'obtient en écrivant :
. La correspondance entre ces deux
représentations s'obtient en écrivant :
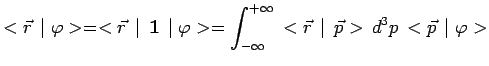 |
soit :
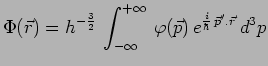 |
On remarque que les éléments de la matrice de changement de base, sont :
Question 3-21 : Montrez que cette matrice est unitaire et expliquez pourquoi elle devait l'être ?
On remarque que les deux fonctions d'onde
![]() et
et
![]() sont transformées de Fourier l'une de l'autre.
sont transformées de Fourier l'une de l'autre.
La décomposition du vecteur ket
![]() représentatif
d'un état sur la base
représentatif
d'un état sur la base
![]() des états propres
d'impulsion :
des états propres
d'impulsion :
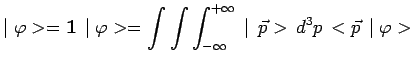 |
permet de préciser quelle est la distribution de probabilité des
valeurs de l'impulsion de la particule dans l'état ![]() . Par application
du principe de Born :
. Par application
du principe de Born :
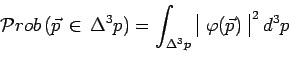 |
Question 3-22 : Soit
![]() la
fonction d'onde représentative de l'état
la
fonction d'onde représentative de l'état ![]() d'une particule (espace à
1 dimension). Calculez la probabilité :
d'une particule (espace à
1 dimension). Calculez la probabilité :
![]() désignant l'impulsion de la particule.
désignant l'impulsion de la particule.
Ainsi dans un tel état quelconque ![]() , aucune des observables n'a une
valeur définie. Les dispersions des valeurs des variables de position
, aucune des observables n'a une
valeur définie. Les dispersions des valeurs des variables de position
![]() sont mesurées par les écarts-types
sont mesurées par les écarts-types
![]() ,
calculées sur la fonction d'onde
,
calculées sur la fonction d'onde
![]() . de même les écarts-types
. de même les écarts-types
![]() , relatives aux composantes de l'impulsion
sont calculées à l'aide de la fonction
, relatives aux composantes de l'impulsion
sont calculées à l'aide de la fonction
![]() . On démontre
mathématiquement que lorsque deux telles fonctions sont transformées de
Fourier l'une de l'autre, les écarts-types satisfont les inégalités :
. On démontre
mathématiquement que lorsque deux telles fonctions sont transformées de
Fourier l'une de l'autre, les écarts-types satisfont les inégalités :
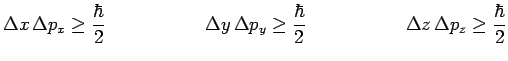 |
On retrouve ainsi les inégalités de Heisenberg.