Particules de spin $\frac{1}{2}$

Les développements précédents concernant les systèmes de spin 0 et 1 peuvent être transposés pour des systèmes de spin intrinsèque quelconque. D'une façon générale, on trouverait que si le système a un spin $s$ , le nombre de ses composantes est égal à $2s+1$ .

En particulier, si les états du système ou de la particule considérée sont repérés par deux fonctions d'onde composantes, le spin de la particule est égal à $\frac{1}{2}$ (cas de l'électron et des nucléons : neutrons et protons).

Dans ce cas $\vec{S}^{~2}$ a pour unique valeur propre $s\,(s+1)\,\hbar^2$ et chaque composante, $S_z$ par exemple, a seulement deux valeurs propres $+\frac{\hbar}{2}$ et $-\frac{\hbar}{2}$ . Nous supposerons ces deux valerus propres non dégénérées et il leur correspond alors les deux vecteurs de base de l'espace de spin :

$$\begin{array}{ccccc} \mid s,s_z> & = & \mid \frac{1}{2},\frac... ... & \mid \frac{1}{2},-\frac{1}{2}> & = & \mid -> \\ \end{array}$$

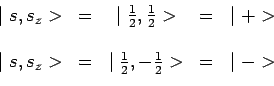Sur cette base la fonction d'onde du système se développe :

$$\mid \Psi> = \Psi_+(\vec{r})\,\mid +>+\Psi_-(\vec{r})\,\mid ->$$

et les composantes du spin $\vec{S}$ admettent la représentation matricielle suivante avec :

$$\sigma_x=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\righ... ...~~~~~~~~~~ \sigma_z=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

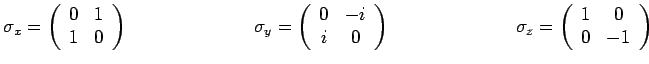Ces matrices appelées matrices de Pauli satisfont aux relations suivantes, comme il est aisé de le vérifier :

$$\sigma_x^2=\sigma_y^2=\sigma_z^2=\sigma_u^2=1$$

$$\sigma_x\,\sigma_y=-\sigma_y\,\sigma_x=i\,\sigma_z$$

$$\sigma_y\,\sigma_z=-\sigma_z\,\sigma_y=i\,\sigma_x$$

$$\sigma_z\,\sigma_x=-\sigma_x\,\sigma_z=i\,\sigma_y$$

$$\mathrm{Tr}~\sigma_x=\mathrm{Tr}~\sigma_y=\mathrm{Tr}~\sigma_z=0$$

$$\mathrm{Det}~\sigma_x=\mathrm{Det}~\sigma_y=\mathrm{Det}~\sigma_z=-1$$

Ainsi, outre les relations de commutations habituelles pour les moments angulaires qui sont les suivantes :

$$[S_x,S_y]=i\hbar\,S_z~\ldots~~\mathrm{etc}$$

on a :

$$[\sigma_x,\sigma_y]=2i\,\sigma_z$$

Les matrices de spin $\frac{1}{2}$ anticommutent deux-à-deux :

$$S_x\,S_y+S_y\,S_x=[S_x,S_y]_+=0~\ldots~~\mathrm{etc}$$

Le fait que l'opérateur $\vec{S}$ jouit des mêmes propriétés de commutation que l'opérateur $\vec{L}$ , image du moment cinétique orbital, explique pourquoi il est à tort considéré comme une sorte de moment cinétique intrinsèque, correspondant à une rotation de la particule sur elle-même, mais une telle image est sans signification, notamment si la particule est ponctuelle.