Etat de spin

Il a déjà été remarqué que les composantes de $\vec{L}$ et celles de $\vec{S}$ agissent sur des vraiables distinctes et indépendantes et par suite commutent toujours :

$$[\vec{L},\vec{S}]=0$$

Dès lors, les variables de base d'une particule se classent donc en deux catégories :

$\imath-$ d'une part, les variables orbitales, fonctions seulement des variables de position $\vec{R}$ et d'impulsion $\vec{P}$ , qui satisfont aux relations de commutation :

$$[R_i,P_j]=i\hbar\,\delta_{ij}~~~~~~~~~~~~~~~(i,j=1,2,3)$$

$\imath\imath-$ d'autre part, les variables de spin, fonctions seulement des composantes de $\vec{S}$ qui satisfont aux autres relations de commutation :

$$[S_i,S_j]=i\hbar\,S_k$$

$i,j,k$ désignant une permutation circulaire de $1,2,3$ ou $x,y,z$ .

Ainsi, pour une particule dotée d'un spin, un E.C.O.C. peut être constitué avec les observables :

$$X,Y,Z,\vec{S}^2,S~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{ou}~~~~~~~~P_x,P_y,P_z,\vec{S}^2,S_z$$

Les vecteurs propres des trois premières observables $\{\mid x,y,z>\}$ ou $\{\mid p_x,p_y,p_z>\}$ engendrent l'espace des états spatiaux ${\mathcal{H}}_{0}$ : le seul considéré jusqu'à maintenant. Par ailleurs les vecteurs propres $\mid s,m>$ des observables $\vec{S}^2$ et $S_z$ engendrent un espace à $2s+1$ dimensions : l'espace ${\mathcal{H}}_{s}$ des états de spin. L'espace complet des états est le produit cartésien des deux précédents :

$$\mathcal{H}=\mathcal{H}_0\otimes\mathcal{H}_s$$

Nous verrons dans le chapitre 4 que ce produit est un produit tensoriel des dexu espaces facteurs.

Un état de la particule pourra donc être représenté par un vecteur ket de la forme :

$$\mid K>=\mid \Psi>\otimes\mid \chi>~~~~~~~~~~~~~~~~~~~~~~~~\mathr... ...hcal{H}_0 \\ & & \\ \mid \chi> & ~~\in~~ & \mathcal{H}_s \\ \end{array}\right.$$

ou encore plus généralement :

$$\mid K>=\sum\limits_{i=1}^m\,C_i\,\mid \Psi_i>\otimes\,\mid \chi_i>~~~~~~~~~~~~~~~~~~~~~~~~C_i\,\in\,\mathbf{C}$$

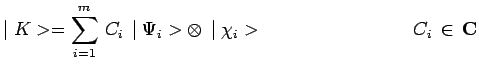$\mid \Psi>$ et $\mid \Psi_i>$ pouvant être eux-mêmes représentés par des fonctions d'onde dans la représentation de Schrödinger, tandis que $\mid \chi>$ et $\mid \chi_i>$ s'expriment sur la base $\mid s,m>$ :

$$\mid \chi>=\sum\limits_{m=-s}^{+s}\,\chi_m\,\mid s,m>~~~~~~~~~~~~~~~~~~~~~~~~ \chi_m\,\in\,\mathbf{C}$$

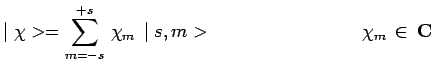de telle sorte que $\chi_m=<s,m\mid \chi>$ . L'état de spin $\mid \chi>$ peut donc être représenté par une matrice colonne $\chi_m$ de $2s+1$ lignes. En particulier si $s=\frac{1}{2}$ on remarque :

$$\mid \frac{1}{2},\frac{1}{2}>=\mid +>=\left( \begin{array}{c}... ...}>=\mid ->=\left( \begin{array}{c} 0 \\ 1 \\ \end{array}\right)$$

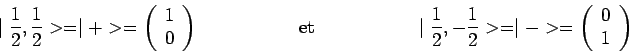Considérons l'état particulier suivant, écrit dans la représentation de Schrödinger :

$$\mid \Psi> = \Psi_+(\vec{r})\,\mid +>+\Psi_-(\vec{r})\,\mid ->$$

On notera que, dans cet état, la probabilité de trouver la particule dans un élément de volume $dV$ centré sur $\vec{r_0}^{~2}$ et dans l'état de spin $S_z=-\frac{\hbar}{2}$ est égale à :

$$\mathcal{P}rob\left(\begin{array}{c} \vec{r}\,\in\,dV \\ S_z=... ...in{array}{\vert c\vert}\Psi_-(\vec{r_0})\\ \end{array}^{~2}\,dV$$

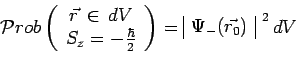Sous forme matricielle l'état $\Psi$ s'écrira encore :

$$\mid \Psi>=\Psi_+\,\left(\begin{array}{c} 1 \\ 0 \\ \end{array}\r... ...\left(\begin{array}{c} \Psi_+(\vec{r}) \\ \Psi_-(\vec{r}) \\ \end{array}\right)$$

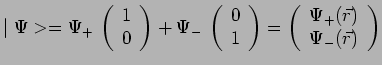L'état d'une particule de spin $s=\frac{1}{2}$ est bien représenté par une fonction d'onde à deux composantes. C'est bien cette considération, qui précédemment, a été utilisée pour introduire la notion de spin.