L'espace
![]() des états de spin, d'une particule de spin
des états de spin, d'une particule de spin ![]() est un espace
à
est un espace
à ![]() dimensions. Dans cet espace tout opérateur, et notamment tout
opérateur de rotation induite, est représenté par une matrice à
dimensions. Dans cet espace tout opérateur, et notamment tout
opérateur de rotation induite, est représenté par une matrice à ![]() lignes et
lignes et ![]() colonnes. D'une façon générale, un tel opérateur
correspondant à une rotation d'un angle
colonnes. D'une façon générale, un tel opérateur
correspondant à une rotation d'un angle ![]() autour d'un axe
autour d'un axe ![]() a
pour expression :
a
pour expression :
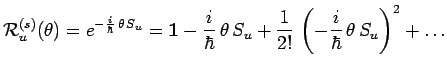 |
Si
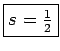 :
:
Dans ce cas on pose
![]() :
:
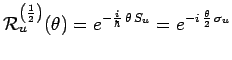 |
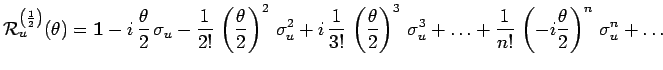 |
Tenu compte des identités de Pauli :
![$\displaystyle e^{-i\,\frac{\theta}{2}\,\sigma_u}=
\left[\mathbf{1}-\frac{1}{2}\...
...t[\frac{\theta}{2}-
\frac{1}{3!}\,\left(\frac{\theta}{2}\right)^3+\ldots\right]$](img2115.png) |
et finalement :
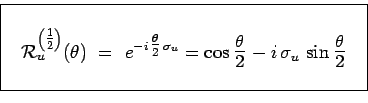 |
et par exemple, en remplaçant les matrices ![]() par leurs
expressions explicites :
par leurs
expressions explicites :
 |
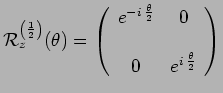 |
Les rotations des états de spin s'obtiennent par application de ces
opérateurs de rotation induite. On remarquera en particulier, que dans une
rotation complète d'angle ![]() , le ket ou la fonction d'onde d'une particule
de spin
, le ket ou la fonction d'onde d'une particule
de spin
![]() change de signe :
change de signe :
 |
Si
![]() :
:
Les expressions des opérateurs
![]() pour une
particule de spin 1 ont été données précédemment. sur
ces expressions on vérifie par exempleIII14 :
pour une
particule de spin 1 ont été données précédemment. sur
ces expressions on vérifie par exempleIII14 :
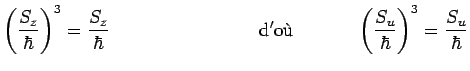 |
car tout axe ![]() de rotation peut être choisi pour axe
de rotation peut être choisi pour axe ![]() .
Il en résulte :
.
Il en résulte :
 |
L'opérateur de rotation induite peut alors être développé suivant les
puissances de l'angle ![]() de rotation autour de l'axe
de rotation autour de l'axe ![]() :
:
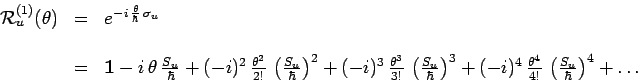 |
ou encore, en regroupant les termes :
On reconnait les développements de
![]() et
et
![]() d'où :
d'où :
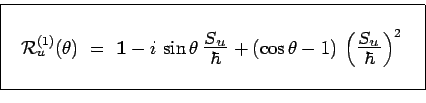 |
et par exemple, sur la base
![]() :
:
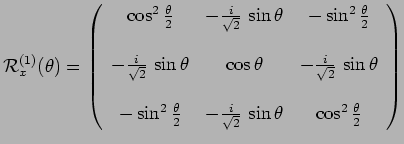 |
Question 3-24 : Calculez les matrices :
Question 3-25 : Une rotation quelconque dans l'espace peut être réalisée en effectuant successivement les trois rotations suivantes :
![]() rotation d'angle
rotation d'angle ![]() autour de
autour de ![]() (
(![]() vient en
vient en
![]() ),
),
![]() rotation d'angle
rotation d'angle ![]() autour de
autour de ![]() (
(![]() vient
en
vient
en ![]() ),
),
![]() rotation d'angle
rotation d'angle ![]() autour de
autour de ![]() (
(![]() vient en
vient en ![]() ),
),
soit :
où
![]() sont les angles d'Euler de la rotation
sont les angles d'Euler de la rotation
![]() . Démontrez :
. Démontrez :