Appelons ![]() l'ensemble de tous les paramètres, autres que
l'ensemble de tous les paramètres, autres que ![]() et
et ![]() ,
connus ou inconnus, dont peut dépendre la probabilité cherchée :
,
connus ou inconnus, dont peut dépendre la probabilité cherchée :
Pour un ensemble de valeurs constantes et fixées de ![]() , cette probabilité
ne peut plus dépendre que de
, cette probabilité
ne peut plus dépendre que de ![]() et
et ![]() . Puisque ces paramètres sont
indépendants et puisque la mesure de
. Puisque ces paramètres sont
indépendants et puisque la mesure de ![]() (respectivement
(respectivement ![]() ) et l'injection
du signal
) et l'injection
du signal ![]() (respectivement
(respectivement ![]() ) constituent deux événements séparés
par un intervalle du genre espace, la probabilité totale correspondante à
ces valeurs fixées de
) constituent deux événements séparés
par un intervalle du genre espace, la probabilité totale correspondante à
ces valeurs fixées de ![]() devient factorisableV18 :
devient factorisableV18 :
Puisque ces paramètres ![]() sont mal connus et éventuellement
variables, ces probabilités ne sont pas mesurables. Toutefois nous admettrons
que les variables
sont mal connus et éventuellement
variables, ces probabilités ne sont pas mesurables. Toutefois nous admettrons
que les variables ![]() admettent une distribution de probabilité
admettent une distribution de probabilité
![]() et que les mesures de corrélation effectuées correspondent
à des mesures moyennes effectuées sur cette distribution :
et que les mesures de corrélation effectuées correspondent
à des mesures moyennes effectuées sur cette distribution :
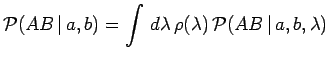 |
Calculons la valeur moyenne du produit ![]() correspondant aux valeurs
correspondant aux valeurs ![]() et
et
![]() , notée :
, notée :
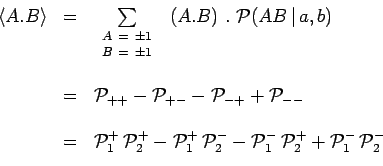 |
de telle sorte que :
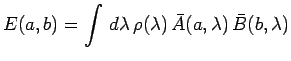 |
avec :
Bien évidemment :
Considérons maintenant un nouvel ensemble de mesures correspondant à un nouveau
couple de valeurs ![]() et
et ![]() :
:
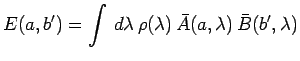 |
On notera que l'on a gardé la même distribution
![]() bien que l'appareillage correspondant à
bien que l'appareillage correspondant à
![]() peut être différentV19 de celui correspondant à
peut être différentV19 de celui correspondant à ![]() . En soustrayant membre
à membre :
. En soustrayant membre
à membre :
![$\displaystyle E(a,b)\pm E(a,b^\prime)=\int\,d\lambda\,\rho(\lambda)\,\bar{A}(a,\lambda)\,
\left[\bar{B}(b,\lambda)\pm \bar{B}(b^\prime,\lambda)\right]$](img3840.png) |
puisque
![]() :
:
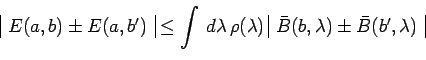 |
Pour deux autres couples
![]() et
et
![]() :
:
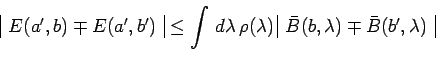 |
d'où, puisque :
et avec :
Il en résulte :
et tenu compte de :
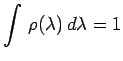 |
on obtient finalement une expression des inégalités de Bell :
et donc a fortiori :
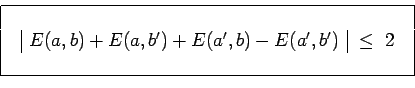 |