d) Cas général

Les résultats précédents peuvent être généralisés, dans le cas où la construction d'une base bien définie de représentation exige l'introduction de plusieurs observables qui commutent $A,B,\ldots,Z$ pour former en E.C.O.C.

Les vecteurs de base sont alors vecteurs propres simultanés :

$$\mid a,b,c,\ldots,z>$$

de cet ensemble d'observables. L'ensemble de ces vecteurs est orthonormalisé comme suit :

$$<a^\prime,b^\prime,c^\prime,\ldots,z^\prime\mid a,b,c,\ldots,z>= \delta(a^\prime,a)\delta(b^\prime,b)\ldots\delta(z^\prime,z)$$

et l'expression formelle de l'opérateur unité en résulte dans le cas général :

$$\mathbf{1}=\underset{a,b,\ldots,z}{\scalebox{1.7}{S}}~\mid a,b,c,\ldots,z><a,b,c,\ldots,z\mid$$

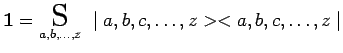dans laquelle le symbole S désigne une sommation sur toutes les valeurs de chacune des variables $a,b,\ldots,z$ , cette sommation étant une somme $\sum$ sur les valeurs discrètes complétées éventuellement par une intégration sur tout un intervalle contenant la partie continue $\Delta$ du spectre. Par exemple :

$$\underset{a,\ldots}{\scalebox{1.7}{S}}~\mid a,\ldots><a,\ldots\mi... ...s_i \mid a_i,\ldots><a_i,\ldots\mid + \int_\Delta \mid a,\ldots>da<a,\ldots\mid$$

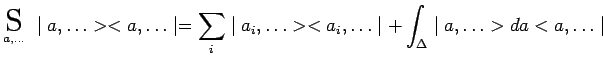Question 1-17 : Démontrez que tout opérateur linéaire L qui commute avec une observable A commute aussi nécessairement avec toute fonction F(A) de cette observable (utiliser les représentations matricielles).

Question 1-18 : Démontrez que tout opérateur linéaire L qui commute avec chacune des observables d'un E.C.O.C. est une fonction des observables de cet E.C.O.C. (utiliser les représentations matricielles).

Question 1-19 : Démontrez que si une observable A et un opérateur linéaire L sont tels que tout opérateur linéaire qui commute avec A commute aussi avec L, alors L est une fonction de l'observable A.

En vertu du résultat précédent, il y a lieu de noter que l'ensemble des observables d'un E.C.O.C. joue, en mécanique quantique, le rôle joué en mécanique classique par les variables dynamiques de base, dont le nombre est égal au nombre de degrés de liberté du système étudié.