Ainsi, les objets théoriques, kets - bras - opérateurs... introduits dans le formalisme de la mécanique quantique peuvent être représentés par divers ensembles de nombres. Plus précisément, à chaque E.C.O.C. correspond une base de l'espace des états et à cette base correspond une représentation du formalisme de la mécanique quantique.
Si les observables ainsi choisies ont des spectres discrets de valeurs propres, les vecteurs et les opérateurs seront représentés par des matrices. Si ces spectres sont continus, les vecteurs et les opérateurs seront représentés par des fonctions, des distributions et des opérateurs fonctionnels.
Changer de représentation, c'est changer de base et donc
d'E.C.O.C. Soit un premier E.C.O.C. contitué des observables
auxquelles correspondent la base de
représenta-tion
notée symboliquement
et un deuxième E.C.O.C. contitué des observables
auxquelles correspondent un deuxième base
notée symboliquement
.
Un même ket 
aura pour composantes les nombres 
dans la première représentation et les nombres 
dans la seconde. Sachant que :
 |
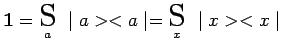on en déduit immédiatement :
 |
 |
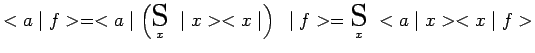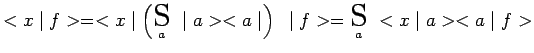Les nombres 
sont les éléments d'une matrice de
changement de base. Par exemple si les spectres sont discrets :
 |
 |
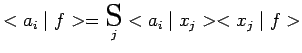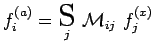On procède de même pour un changement de représentation des opérateurs :
 |
 |
 |
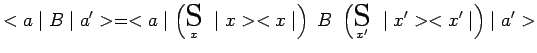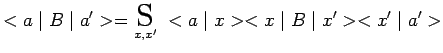que l'on peut noter symboliquement :
 |
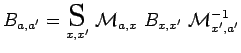Très prochainementI31 nous étudierons deux
exemples de telles représentations, admettant pour vecteurs de
base, l'une, les états propres des observables position
et l'autre, les états propres des observables
impulsion
.